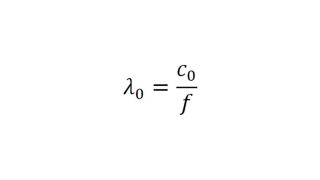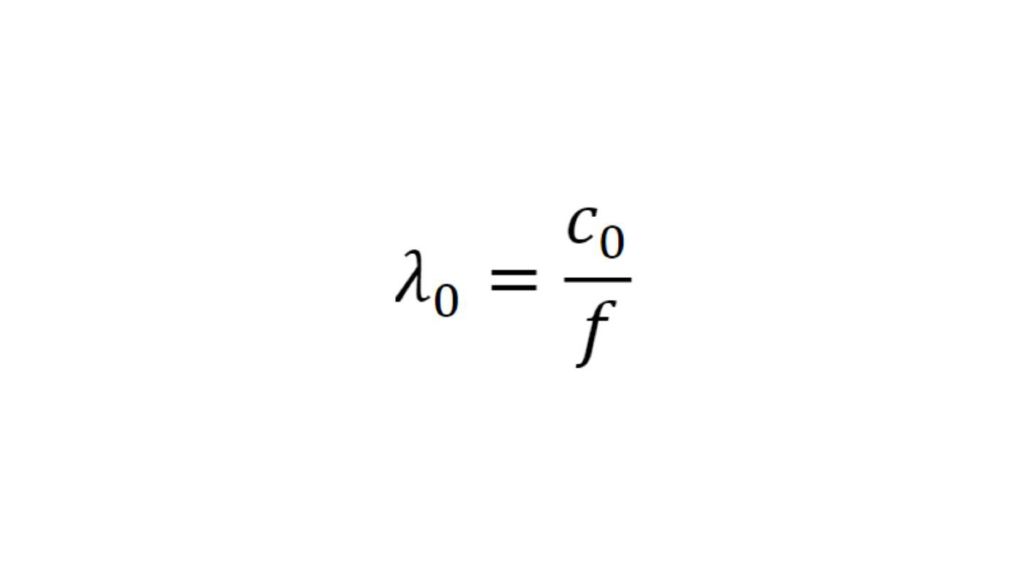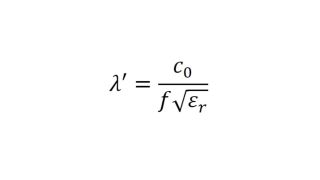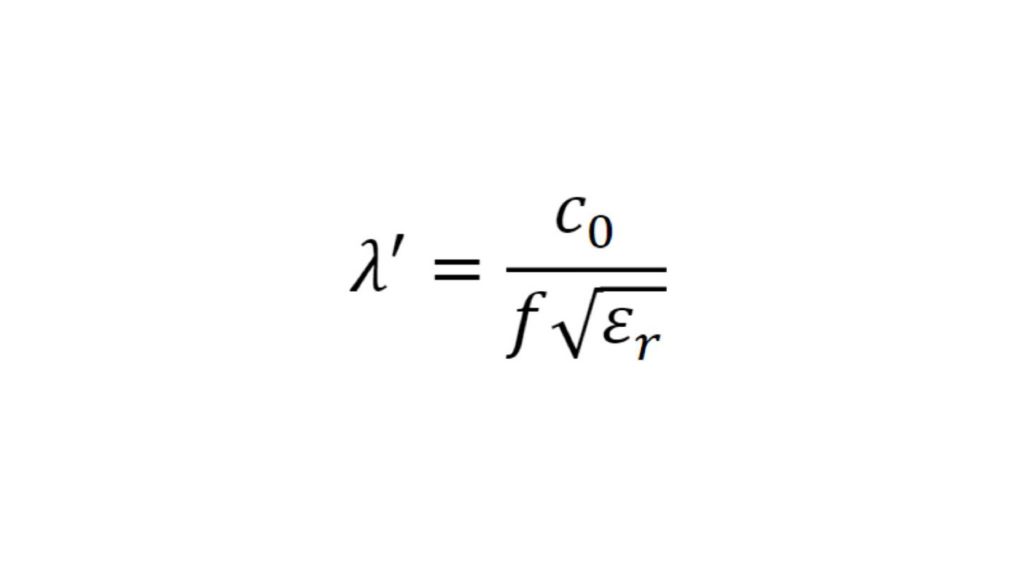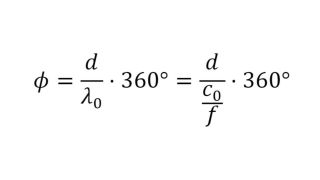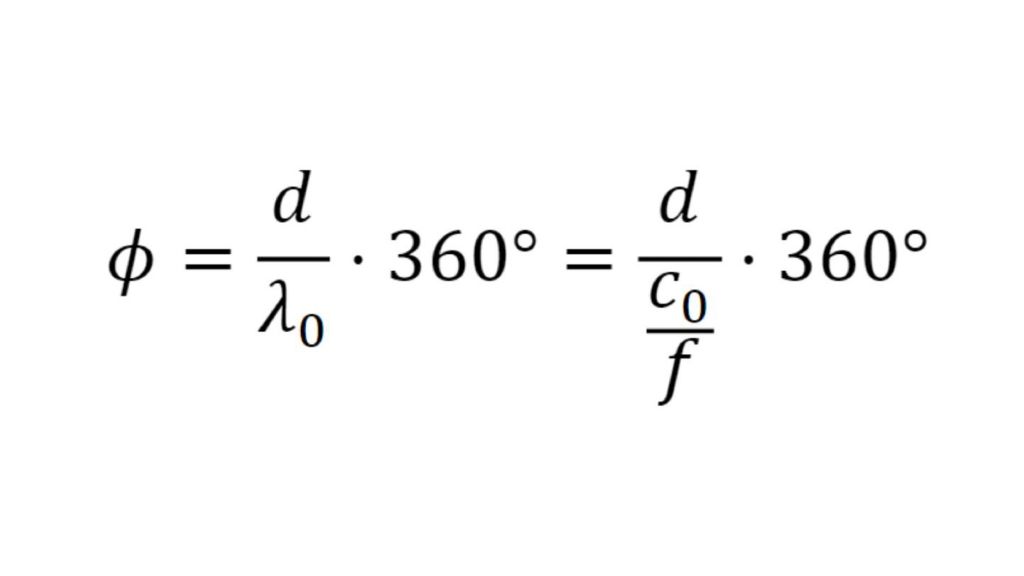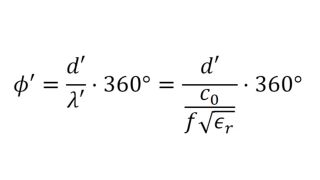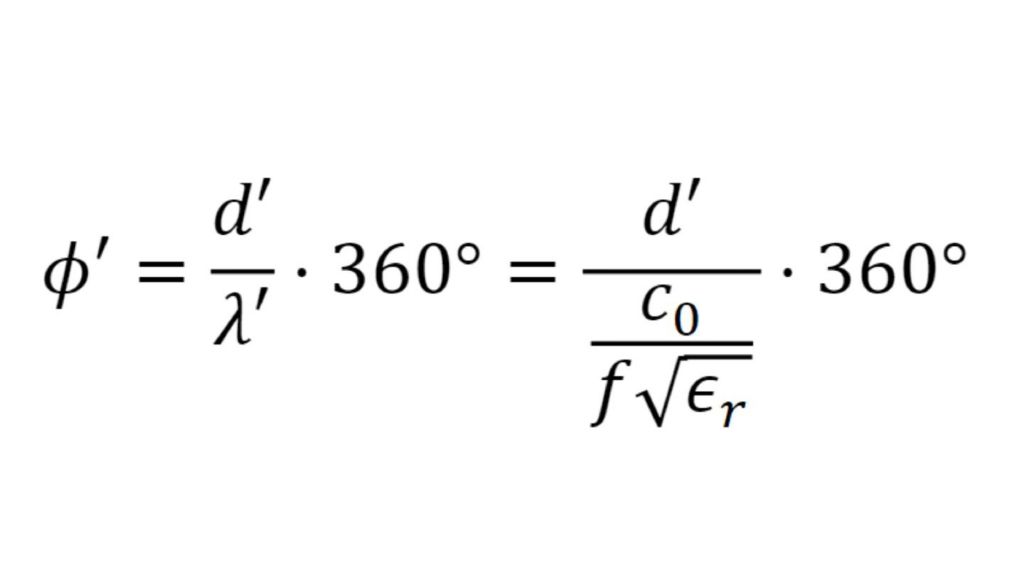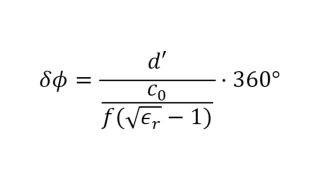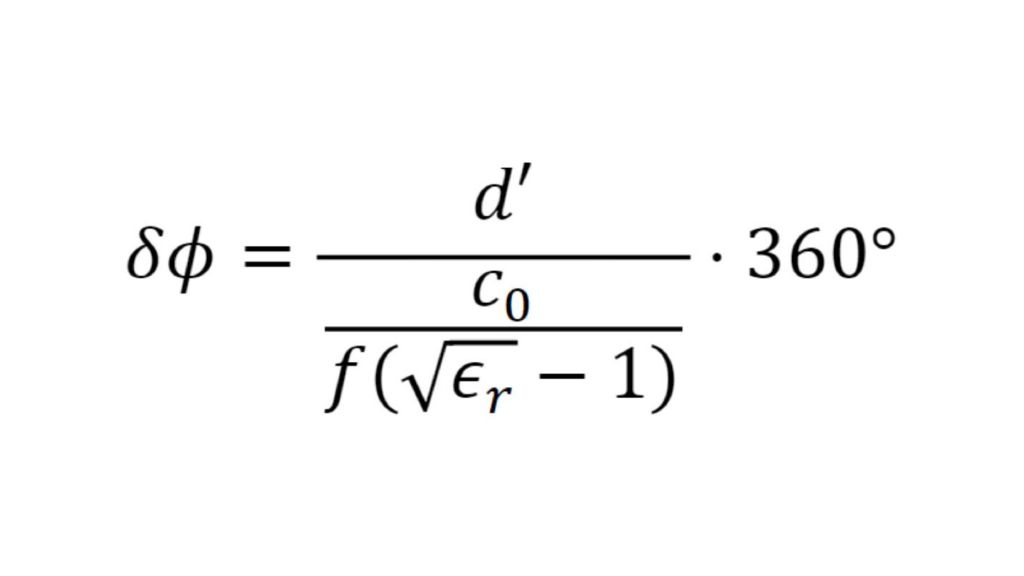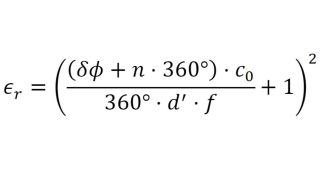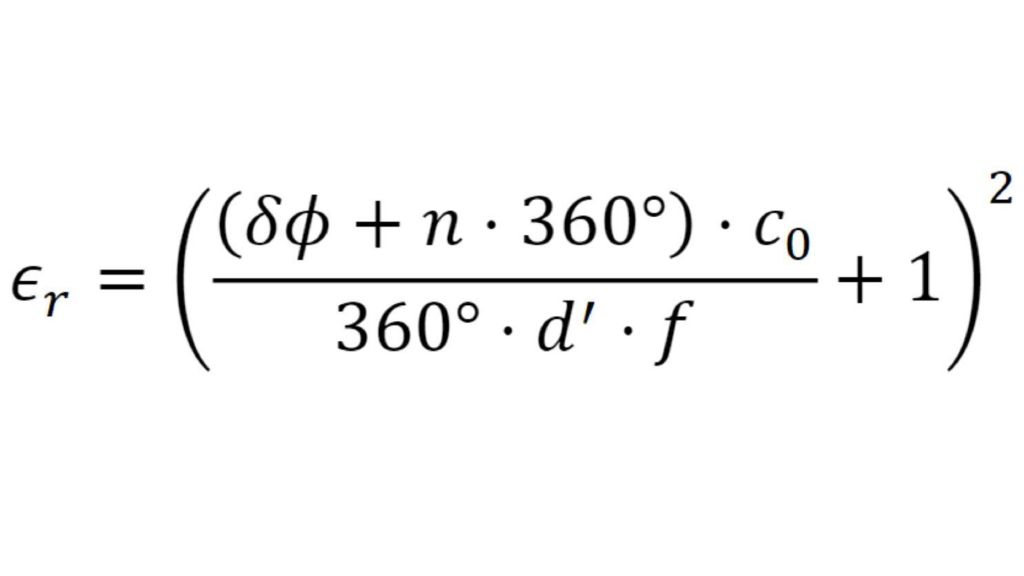Charakterisierung der Materialeigenschaften von Polymeren für Automotive-Anwendungen

Ihre Anforderung

Stoßfänger von Fahrzeugen bestehen für gewöhnlich aus mehreren Schichten: dem strukturellen Basismaterial, darauf der Grundierung, dann dem Farblack und schließlich einem Klarlack, der die oberste Schicht bildet. Bei dem strukturellen Basismaterial handelt es sich meistens um Polypropylen (PP) oder Polycarbonat (PC). Es gibt dem Stoßfänger seine Form. Das Basismaterial ist oft die dickste Schicht, hat jedoch nicht unbedingt auch den größten Einfluss auf das Radarsignal. Die Basisschicht kann mit verschiedenen Füllstoffen angepasst werden, um UV-Widerstand, Steifigkeit, Radardämpfung usw. zu verbessern. Die Grundierung ist die zweite Schicht und unterstützt die Haftung des Farblacks auf dem Basismaterial.

Die Grundierschicht ist in der Regel nur einige Mikrometer dick. Bei der Messung der Dicke dieser sowie der weiteren Schichten ist ein Unsicherheitsfaktor nur schwer zu vermeiden.

Die dritte Schicht ist der Farblack, der auf die Grundierung aufgetragen wird. Die Dicke dieser Lackschicht hängt von ihrem Deckvermögen ab. Normalerweise ist sie aber sehr dünn.

Zum Schutz dieses Farblacks vor Umwelteinflüssen wird als vierte und letzte Schicht ein Klarlack aufgetragen.

Um die elektromagnetischen Eigenschaften eines Stoßfängers beurteilen zu können, werden genaue Informationen über die verschiedenen Schichtdicken benötigt. Für diese Messung kommt ein Rasterelektronenmikroskop zum Einsatz (siehe Bild 1).

Alle Schichten müssen unabhängig voneinander charakterisiert werden. In der folgenden Beschreibung verwenden wir vier verschiedene Proben, um zu einer Charakterisierung aller vier Schichten zu gelangen:

• Zunächst wird nur das Basismaterial analysiert
• Anschließend wird die Grundierung auf das charakterisierte Basismaterial aufgetragen und analysiert
• Im dritten und vierten Schritt gehen wir nach dem gleichen Konzept vor – das heißt, es wird jeweils die nächste Schicht auf die vorherige aufgetragen

Für die Mikroskopaufnahme muss die Probe zerstört werden. Alle oben genannten Messungen müssen im Voraus durchgeführt werden. Im folgenden Abschnitt befassen wir uns mit der erforderlichen HF-Analyse der Proben.

Typische Frequenz eines Automotive-Radars: f_radar = 76,5 GHz, Wellenlänge: λ₀ = 3,92 mm.

Die Wellenlänge innerhalb eines gegebenen Materials mit der relativen Permittivität ε_r lässt sich dann berechnen zu:

Bei der Polypropylen-Plattenprobe (PP) mit ε_r ~ 2,5 erhalten wir entsprechend für die Wellenlänge: λ_PP = 2,34 mm. Da eine höhere Permittivität kürzere Wellenlängen bewirkt, kann sie anhand der gemessenen Phase berechnet werden, wenn die Dicke des getesteten Materials (material under test, MUT) bekannt ist. Das allgemeine Verfahren ist unten beschrieben.

Berechnung der Permittivität mit relativen Phasendifferenzen

Der R&S®QAR50 ist für die Wellenausbreitung in der Luft normalisiert. Befindet sich irgendein anderes Material zwischen den beiden Clustern, verändert sich die Phase an den Empfangsantennen entsprechend. Zur Charakterisierung der Probe benötigen wir die vom MUT innerhalb des Messpfads verursachte Phasendifferenz.

Zum Verständnis: Die Phase Φ in Grad, gemessen über eine Distanz d im freien Raum, berechnet sich wie folgt:

Die Phase Φ’ beim Durchlaufen eines Materials der Dicke d’ ergibt sich zu:

Die Phasenänderung δΦ, die vom R&S®QAR50 gemessen wird, ist die Differenz zwischen Φ und Φ’ und gleich:

Für eine 2,92 mm dicke PVC-Platte mit einer geschätzten Permittivität ε_r von ungefähr 2,5 ergibt sich eine erwartete Phasendifferenz δΦ von fast 158°.

Da wir die Phasendifferenz δΦ mit dem R&S®QAR50 messen und die Permittivität εr berechnen wollen, ist die Gleichung oben umzuformen in:

Der berechnete Wert für die Permittivität ist jedoch nicht eindeutig – die Phasendifferenz könnte nämlich auch Vielfaches von 360° enthalten. Alle möglichen Lösungen können für n Σ N₀ berechnet werden.

Bei mehrschichtigen Proben müssen alle Schichten außer der zu bestimmenden Schicht vorab charakterisiert werden. Nur dann können die bekannten Schichten rechnerisch kompensiert oder „herausnormalisiert“ werden.

Die Software des R&S®QAR50 vereinfacht die Berechnung. Der Permittivitätsrechner nutzt präzise Phasenmessergebnisse des R&S®QAR50, wie im Beispiel unten dargestellt.

Beispiel der Charakterisierung einer lackierten Stoßfängerprobe

Wir verwenden den gleichen Probensatz wie oben. Die Dicken der verschiedenen Schichten sind bekannt und es liegen Platten mit einzelnen Schichten zur Charakterisierung vor. Die Dicken der einzelnen Schichten sind in Bild 1 angegeben.

Die PP-Basisplatte hat eine Dicke von 2,92 mm. Die gemessene Phasendifferenz beträgt etwa –153° bei 76,5 GHz. Mit den Messergebnissen als Eingabeparameter berechnet das Tool eine Permittivität ε_r von 2,47 für diese spezielle Platte. Bild 2 zeigt das Berechnungsergebnis der Software.

Mit dem unten beschriebenen HF-Berechnungstool kann die optimale Dicke d_opt aus den Minima der Reflexions- und Transmissionsdämpfung abgeleitet werden. Die Reflexionsminima korrelieren mit der Resonanzfrequenz der Probe und liegen bei Vielfachen der halben Wellenlänge im Material:

Um die restlichen Schichten zu charakterisieren, muss das Basismaterial herausgerechnet werden. Da die Permittivität des Materials nun bekannt ist, kann auch die Grundierungsplatte normalisiert werden.

In der Software wird eine Normalisierungsschicht hinzugefügt und das nächste Messergebnis geladen.

Die Normalisierung kann entweder auf Grundlage einer vorherigen Messung oder durch manuelles Hinzufügen einer Schicht mit definierter Dicke und Permittivität erfolgen. In unserem Beispiel hat die Normalisierungsschicht eine Dicke von 2,92 mm. Die Permittivität ε_r = 2,47 wird manuell hinzugefügt und auf der rechten Seite des Tools visualisiert. Basierend auf der gemessenen Grundierungsdicke (siehe Bild 1) und der vom R&S®QAR50 gemessenen Phasenverschiebung von 5,3° beträgt die geschätzte Permittivität für die Grundierung ε_r = 18,3. Das Ergebnis ist in Bild 3 zu sehen.

Sobald die zweite Schicht charakterisiert ist, können die verbleibenden Schichten mit den oben beschriebenen Schritten geschätzt werden. Die charakterisierten Schichten werden zur Normalisierung hinzugefügt und das Tool berechnet die unbekannte Permittivität.

Da die Schichtdicke zwischen den Proben unterschiedlich sein kann, ist beim Hinzufügen von Normalisierungsschichten Vorsicht geboten. Bild 4 zeigt eine Aufnahme der Proben von einem optischen Mikroskop. Bei der Zwischenprobe Nr. 3 (zur Charakterisierung der Farblackschicht) und der Probe Nr. 4 (zur Charakterisierung der Klarlackschicht) sind erhebliche Unterschiede in der Dicke der Farblackschicht erkennbar.

Einfluss der Messungenauigkeit
Lassen Sie bei der Dickenmessung Sorgfalt walten, da beide Werte einen starken Einfluss auf die berechnete Permittivität haben. Bild 5 und 6 veranschaulichen die Auswirkungen ungenauer Dicken- und/oder Transmissionsphasenmessungen. Auf Basis der obigen Messungen ergibt sich für eine Beschichtung mit einer Dicke von d = 17,6 μm und einer Phasenverschiebung von ∆φ = –5,3° eine Permittivität mit einem εr von etwa 18,3. Um den Einfluss ungenauer Phasen- und Dickenmessungen zu veranschaulichen, werden beide Parameter für typische Messgenauigkeiten ausgewertet: ±2 μm für die Dickenmessung und ±1° für die Transmissionsphase. Bild 5 zeigt, wie die daraus berechnete relative Permittivität stark variiert, wenn die Messergebnisse ungenauer werden. Gehen Sie beim Messen der HF-Eigenschaften eines Materials und beim Bestimmen der Schichtdicke entsprechend sorgfältig vor.

In Bild 6 hat das Probensubstrat eine Permittivität von 2,42 und eine Dicke von 2,92 mm. Für diese Dickenmessung wurde ein Mikrometer verwendet und die Messunsicherheit beträgt nun ±20 µm. Die Phasengenauigkeit bleibt identisch, da für die Messung dasselbe Gerät verwendet wurde.

Bei Werkstoffen mit geringerer Permittivität und einer Dicke deutlich über der Messunsicherheit (z. B. PC oder PP) ist der Effekt weniger ausgeprägt.

Optimierung der dielektrischen Eigenschaften
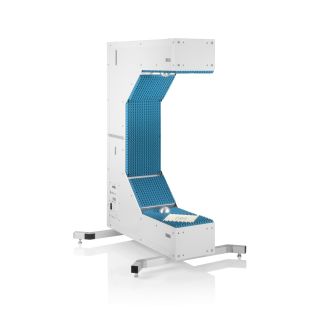
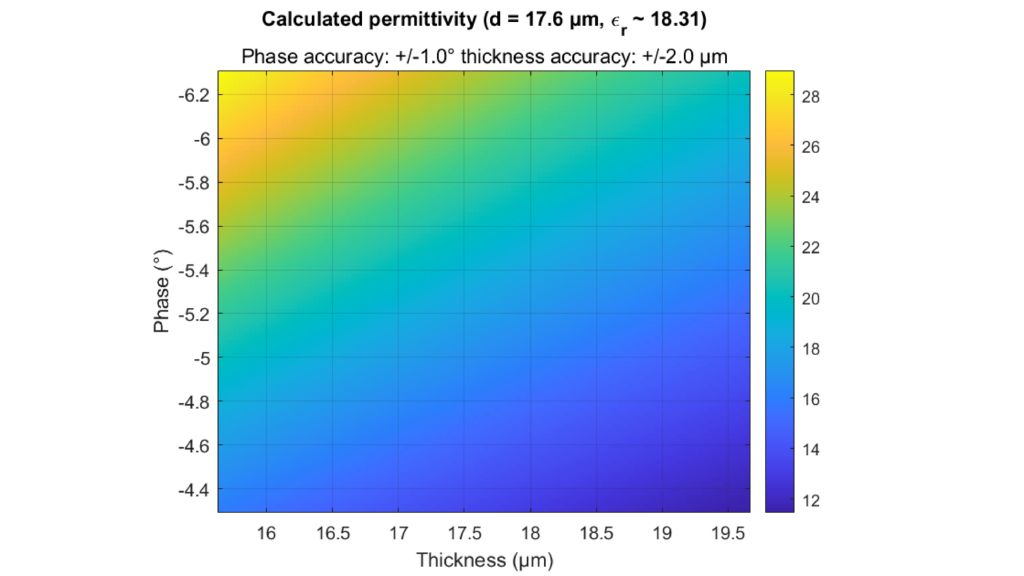
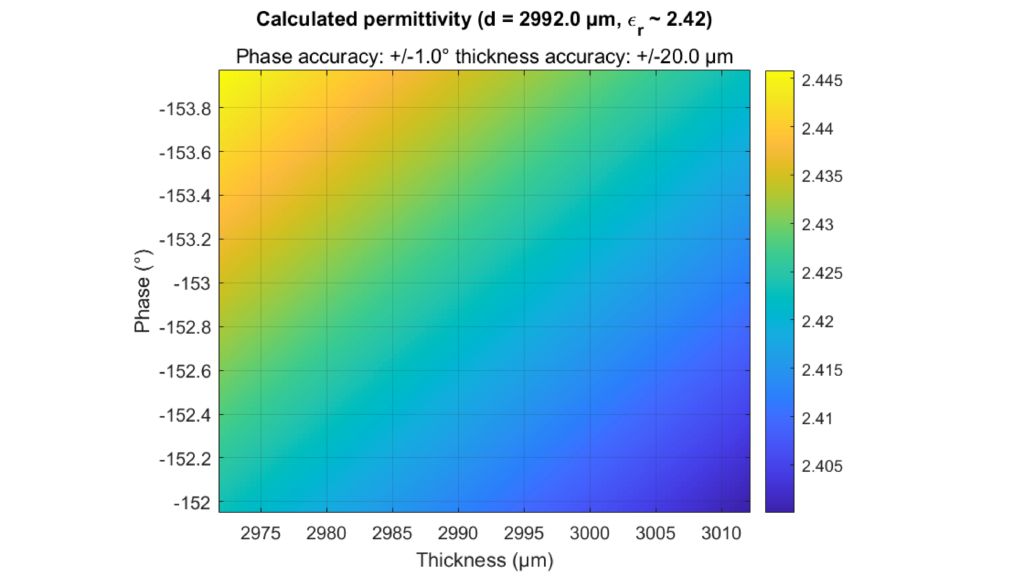
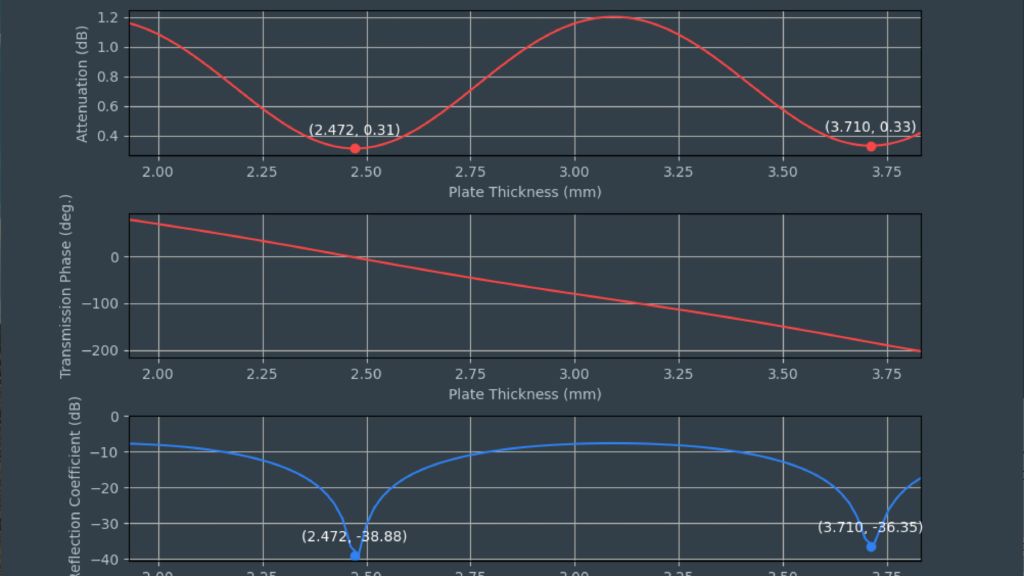
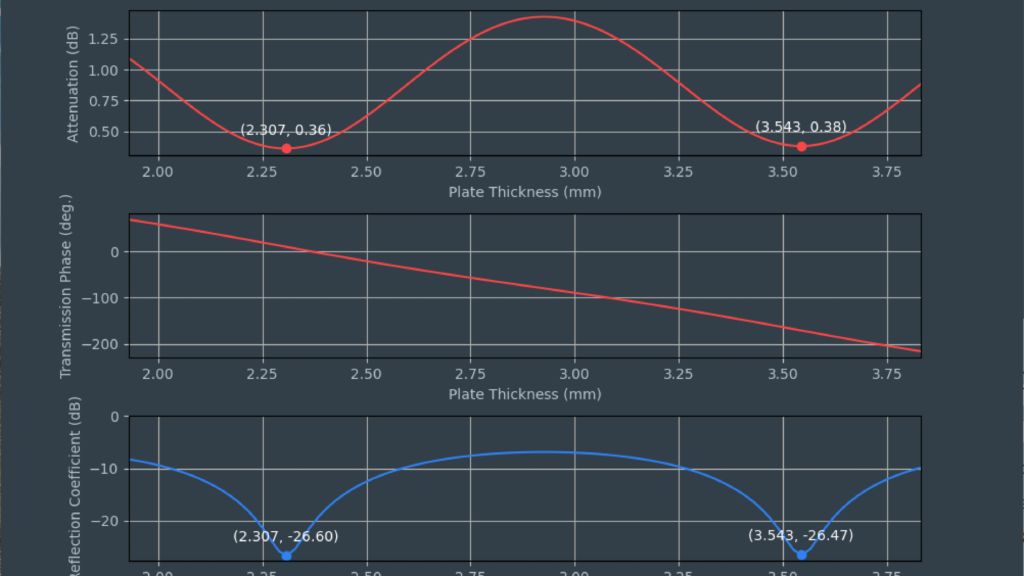
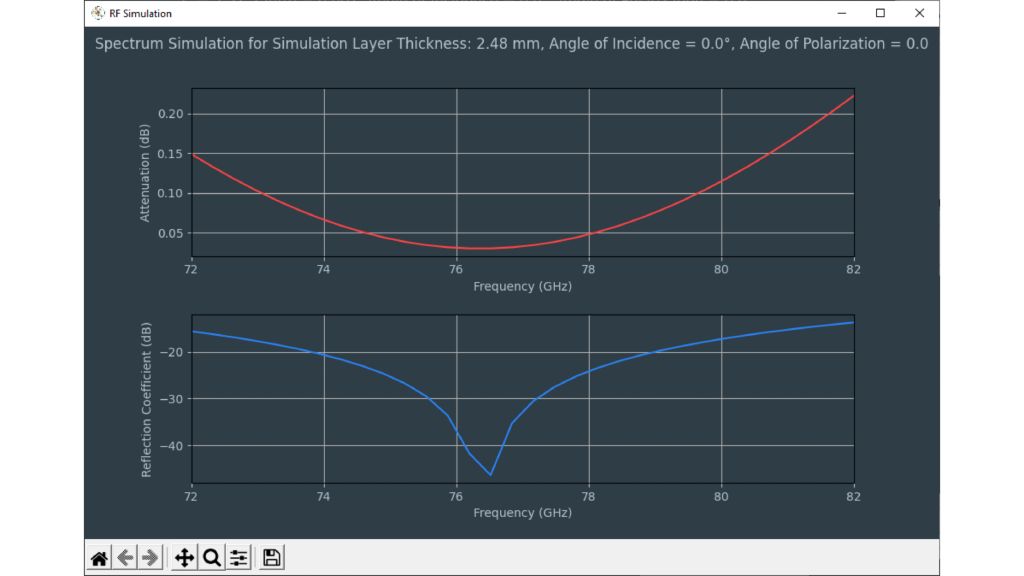
Um Materialien und Materialstapel zu simulieren und ein virtuelles Duplikat eines Radoms zu erstellen, müssen die Permittivität und der Verlustfaktor bekannt sein. Die relative Permittivität εr korreliert mit dem Kompressionsfaktor der Wellenlänge im Material, während der tan δ (Verlustfaktor) die spezifische Dämpfung eines durch die Schicht übertragenen Signals charakterisiert.

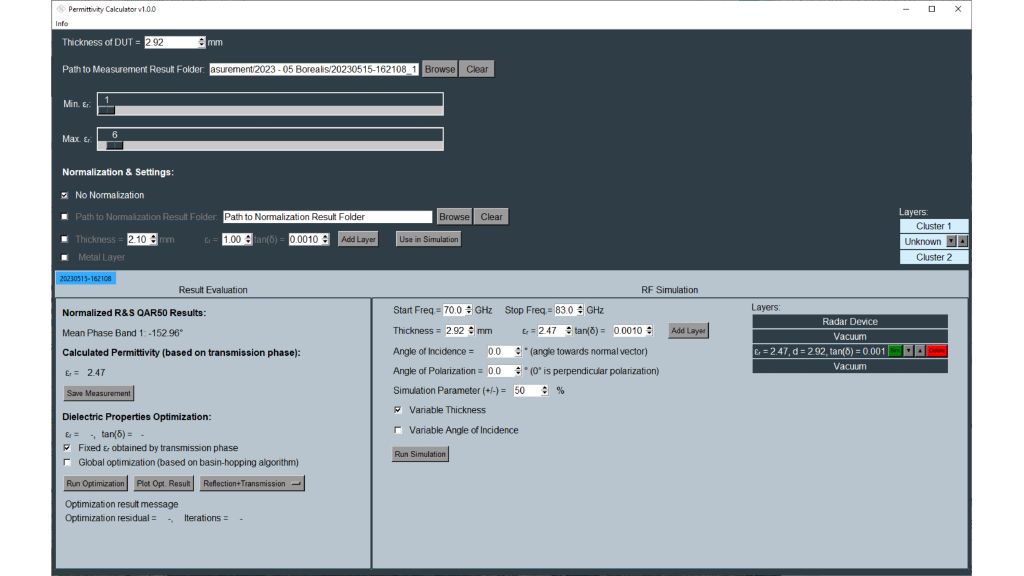
Der Permittivitätsrechner von Rohde & Schwarz lässt sich für beide Parameter nutzen und eignet sich ideal für Radomschicht-Simulationen.

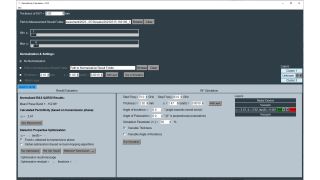
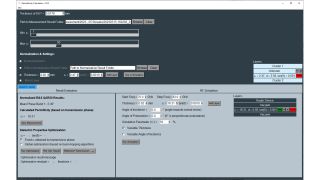
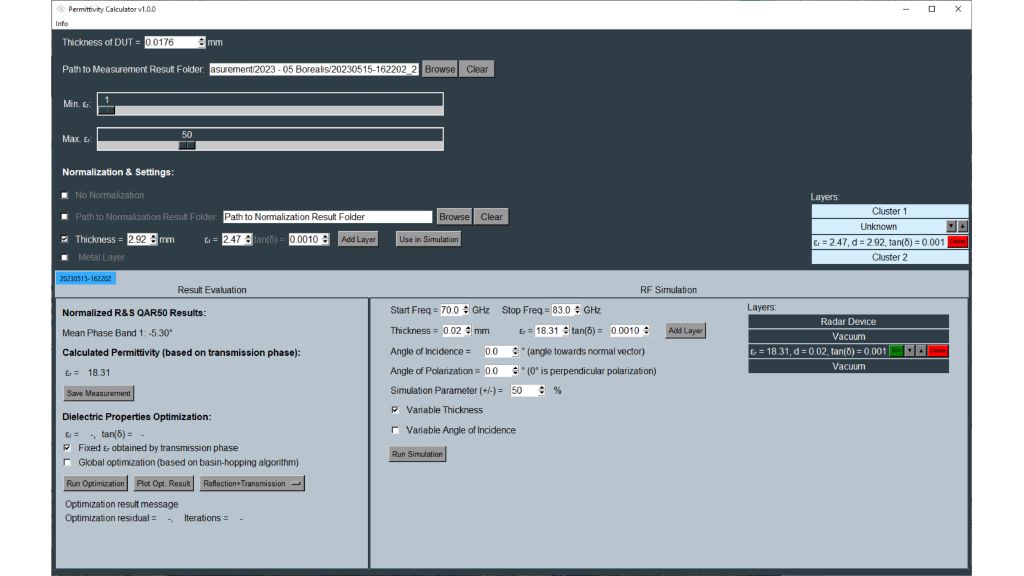
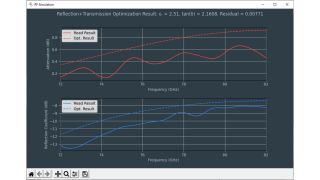
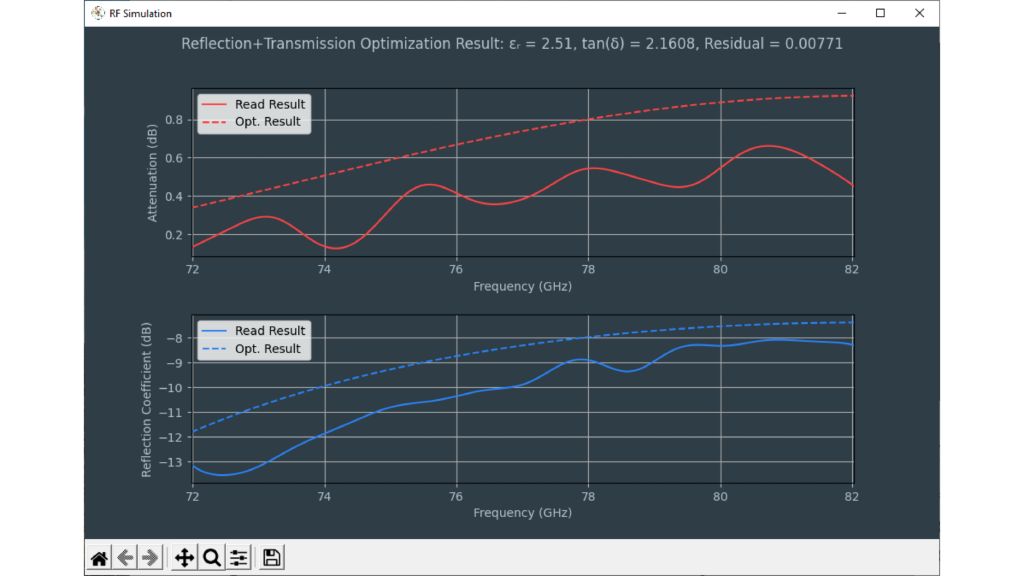
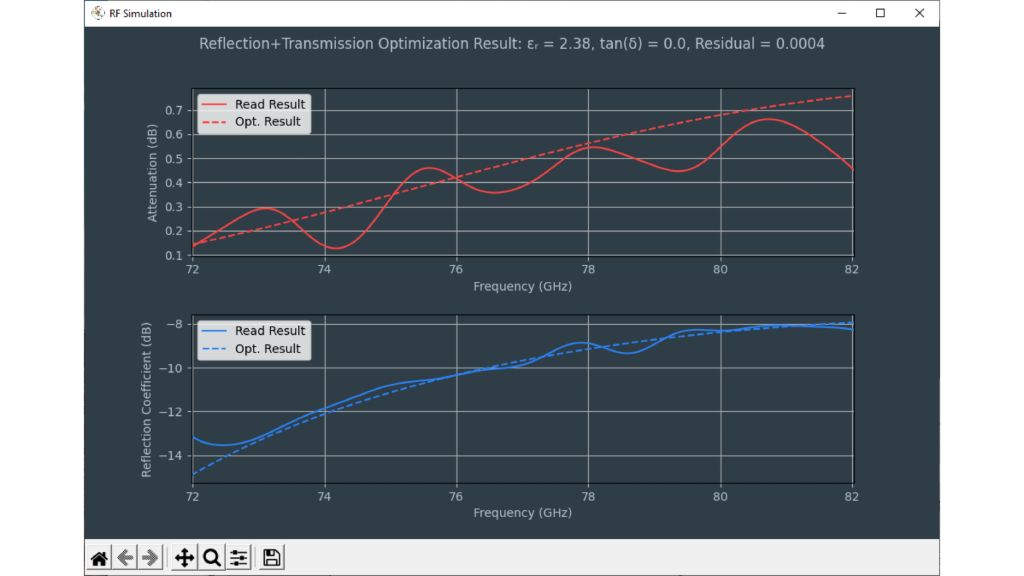
Die Tools zur Schätzung der dielektrischen Eigenschaften befinden sich links unten in der Permittivitätsrechner-Software. Der Rechner verwendet einen Optimierer, um auf Basis der Permittivität und der Verlustfaktoren die beste Übereinstimmung zwischen gemessenen und berechneten Frequenzgängen zu finden. Der Benutzer kann über ein Kontrollkästchen zwischen verschiedenen Berechnungsmethoden wählen:

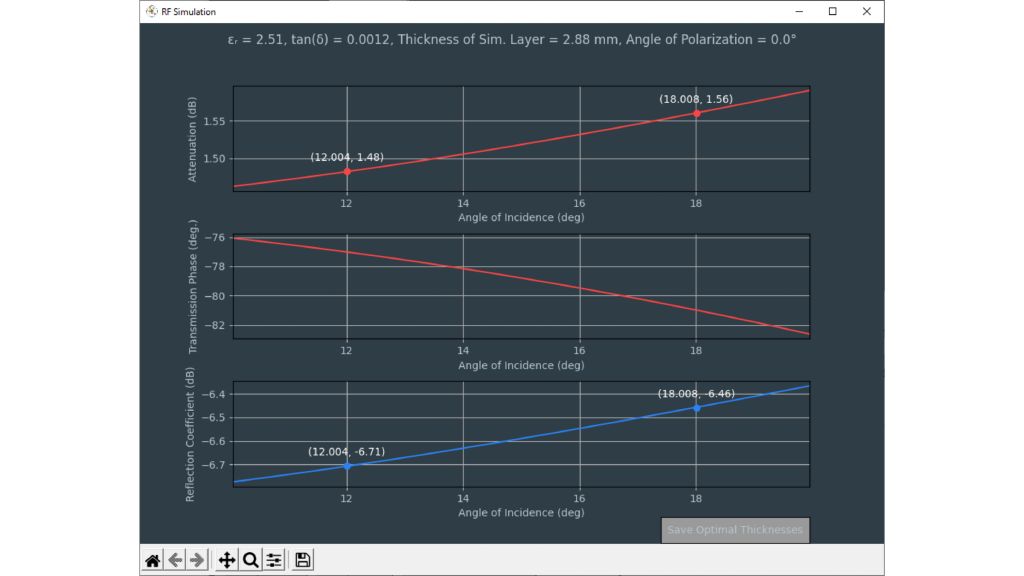
• Im Modus „Fixed εr obtained by transmission phase“ wird nur tan δ optimiert, während die relative Permittivität konstant gehalten wird.
• Wenn Sie das Kontrollkästchen deaktivieren, hat der Optimierer mehr Freiheit zur Verbesserung der relativen Permittivität – die anhand der Transmissionsphase berechnete relative Permittivität dient als Anfangswert.

Beide Methoden führen bei den meisten Materialien zu sehr ähnlichen Ergebnissen. Die Transmissionsphase kann sehr genau gemessen werden und ist immer ein guter Ausgangspunkt für die Optimierung.

Die Option „Optimize using logarithmic scale (dB)“ bewirkt, dass der Optimierer auf Basis einer logarithmischen Kurve arbeitet – dies erhöht die Genauigkeit der Schätzung bei Materialien mit Resonanzen im Frequenzbereich des R&S®QAR50.

Bei der globalen Optimierung werden mehrere, zufällig verteilte Startwerte nahe der berechneten Permittivität verwendet, um lokale Minima zu vermeiden.

Für kundenspezifische Anwendungen stehen die Reflexionskurven aus Cluster 1 (S₁₁) oder Cluster 2 (S₂₂) zur Verfügung.

Die gemessenen und berechneten Frequenzgänge können nach der Optimierung grafisch dargestellt werden. Mit der Funktion „Plot Opt. Results“ lässt sich der Frequenzgang sowohl für das gemessene Material (durchgezogene Linie) als auch für das virtuelle Material (gestrichelte Linie) anhand der zuvor berechneten Materialeigenschaften darstellen. Die Gültigkeit der Ergebnisse beider Methoden muss vom Benutzer überprüft werden. Bild 7 und 8 zeigen die erzeugten Diagramme. Bild 7 wurde mit fester Permittivität anhand der Transmissionsphase generiert. Bild 8 wurde durch Optimierung sowohl der Permittivität als auch der Verlustfaktoren zur Ermittlung des am besten geeigneten Frequenzgangs erstellt.

Zur Abschätzung des Verlustfaktors wird das zuvor mit dem R&S®QAR50 gemessene Material als Beispiel verwendet.

Zur qualitativen Bewertung wird im Diagramm der verbleibende Optimierungsfehler angegeben. Je kleiner dieser Fehler, desto besser die Anpassung. In unserem Beispiel ist das Ergebnis bei Optimierung sowohl von Permittivität als auch Verlustfaktor etwas besser. Die gewonnenen Ergebnisse lassen sich für Simulationen im Schichtoptimierungstool verwenden.

Schichtoptimierungstool

Das Schichtoptimierungstool auf der rechten Seite des Permittivitätsrechners wird mit dem Laden einer gültigen R&S®QAR50 Messung aktiviert. Mit diesem Tool können mehrere Lackschichten simuliert und die Auswirkungen von Unterschieden in der Schichtdicke bewertet werden.

Die Start- und Stoppfrequenz legen die für eine Anwendung verwendeten Radarbänder fest. Ein digitaler Zwilling eines Teils wird mit den zuvor ermittelten Materialparametern für eine Platte mit einer Schicht erstellt. Über die Schaltfläche „calculate optimal thickness“ lässt sich eine HF-Simulation der Schichten durchführen. Die Berechnungsergebnisse für das Probenmaterial und die Dicke sind in Bild 9 dargestellt.

In Bild 9 beträgt die optimale Dicke für eine Platte mit einer Schicht 2,47 mm. Die Dicke gilt für unlackierte Radarabdeckungen. Gehen wir der Einfachheit halber davon aus, dass statt drei Schichten (Grundierung, Lack und Beschichtung) nur eine einzige Schicht auf das Basismaterial aufgetragen wurde. Die hinzugefügte Schicht ist d = 20 μm dick und hat ein ε_r von 15 mit einem tan δ von 0,02. Diese Schicht entspricht einem typischen Lack, wie er in der Automobilindustrie Verwendung findet.

Die Herausforderung ist immer noch dieselbe: Wir benötigen die optimale Basismaterialstärke für eine einzelne Lackschicht. Nachdem wir die Schicht dem HF-Simulationstool hinzugefügt haben, können wir die gleichen Berechnungen wie in Bild 9 durchführen. Nehmen wir an, die Dicke der Lackschicht steht fest und wir möchten die optimale Dicke für die Basisschicht bestimmen. Bild 10 zeigt das Ergebnis der HF-Simulation.

Trotz ihrer geringen Dicke weist die Schicht eine hohe Permittivität auf und beeinflusst die Radar-Performance deutlich – dieser Effekt ist in der Simulation klar erkennbar. Statt 2,47 mm für die unlackierte Platte wäre die optimale Dicke nun 2,31 mm.

Das gleiche Verfahren lässt sich auch für alle übrigen Schichten anwenden, sodass die Dicke der Stoßfängerschichten (oder anderer Schichten) optimiert werden kann.

Eine weitere nützliche Funktion kann aktiviert werden, indem Sie die Maus über einen bestimmten Dickenpunkt im Diagramm bewegen und „n“ drücken. Dadurch wird ein frequenzaufgelöstes Diagramm für diese spezifische Dicke erstellt. Der Frequenzbereich wird vom Benutzer im Hauptfenster des Permittivitätsrechners definiert.

Die oben beschriebenen Simulationsergebnisse können für unterschiedliche Dicken und Simulationswinkel berechnet werden. Wir bleiben bei einer vereinfachten lackierten Platte, um die Auswirkungen des Einbauwinkels der Abdeckung relativ zum Radar auf die Performance zu veranschaulichen. Mit der Permittivitätsrechner-Software kann dieser Effekt ermittelt werden.

Durch Variieren des Einbauwinkels zwischen 10° und 20° (typische Einbauwinkel in Kraftfahrzeugen) wird der Einfluss des Einfallswinkels deutlich.

Der Einfallswinkel und die Polarisation des elektrischen Felds relativ zum Einfallswinkel wirken sich auf die optimale Dicke und Optimierung aus. Mit dem Permittivitätsrechner können die Auswirkungen des Polarisationswinkels der eingehenden elektromagnetischen Welle simuliert werden. 0° entspricht einer senkrechten Polarisation zwischen der Einfallsebene und dem elektrischen Feld der eingehenden elektrischen Welle

Fazit

In Kombination mit dem R&S®QAR50 bildet der Permittivitätsrechner die ideale Toolchain für die Over-the-Air-Materialcharakterisierung. Anhand von Transmissionsdämpfungs-, Phasen- und Reflexionsmessungen können die relative Permittivität und der Verlustfaktor für das getestete Material berechnet werden. Mit dem leistungsfähigen HF-Simulationstool lässt sich die Dicke jeder der Schichten so anpassen, dass das Radom für den Frequenzbereich von Automotive-Radaren optimal abgestimmt ist.

Sie können die Permittivitätsrechner-Software kostenlos von der R&S®QAR50 Website herunterladen:

www.rohde-schwarz.com/de/software/qar50/