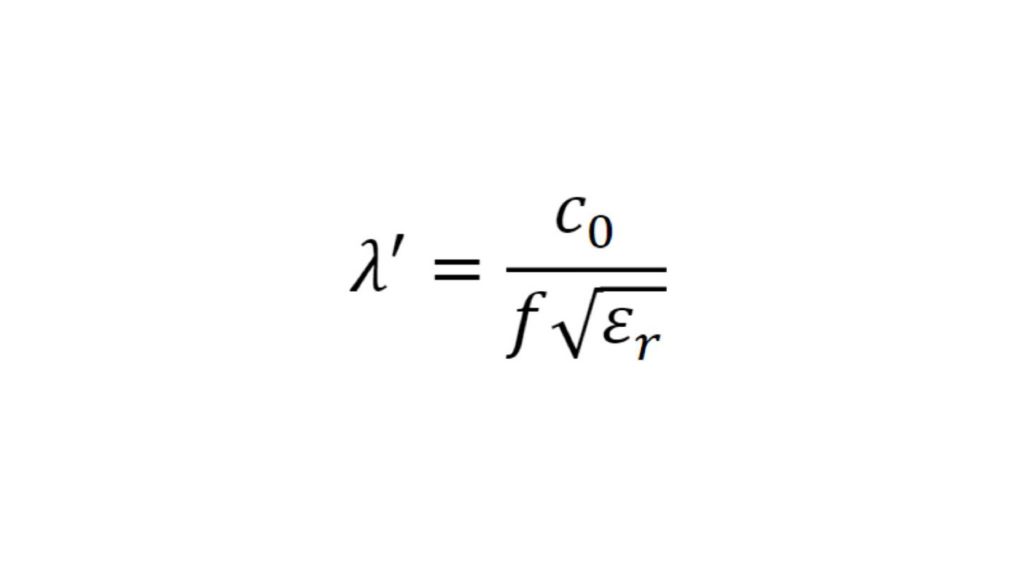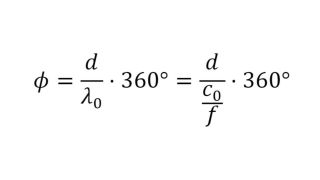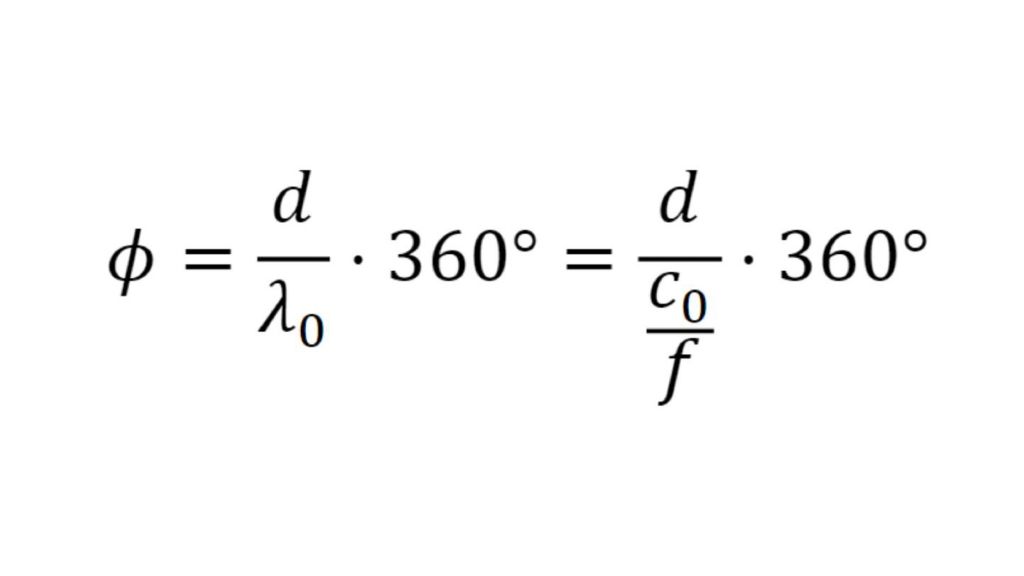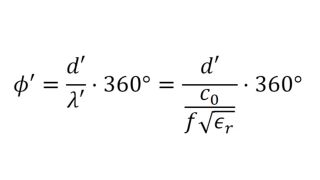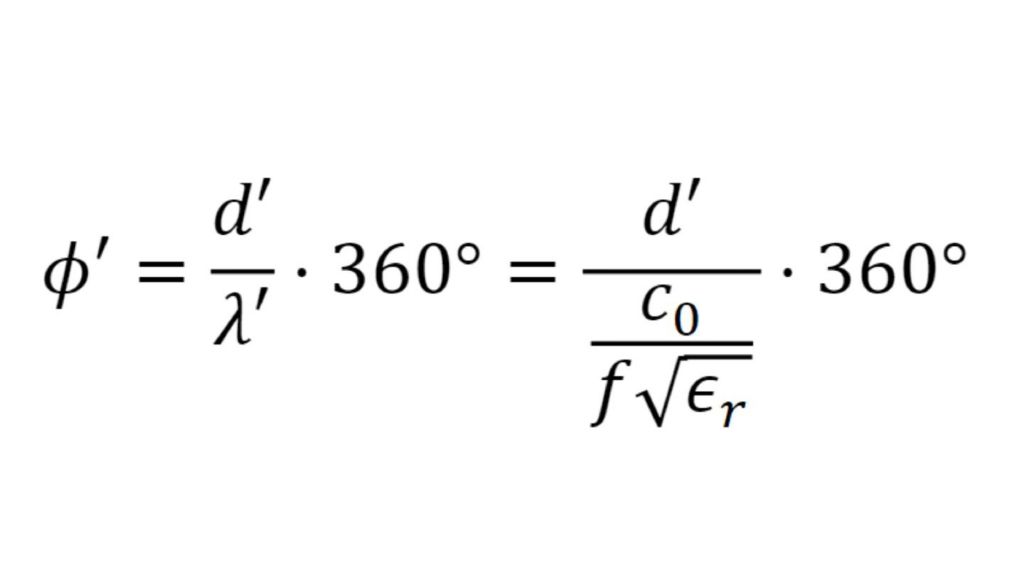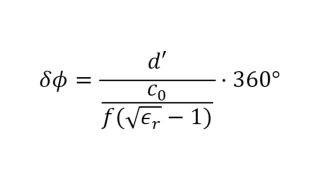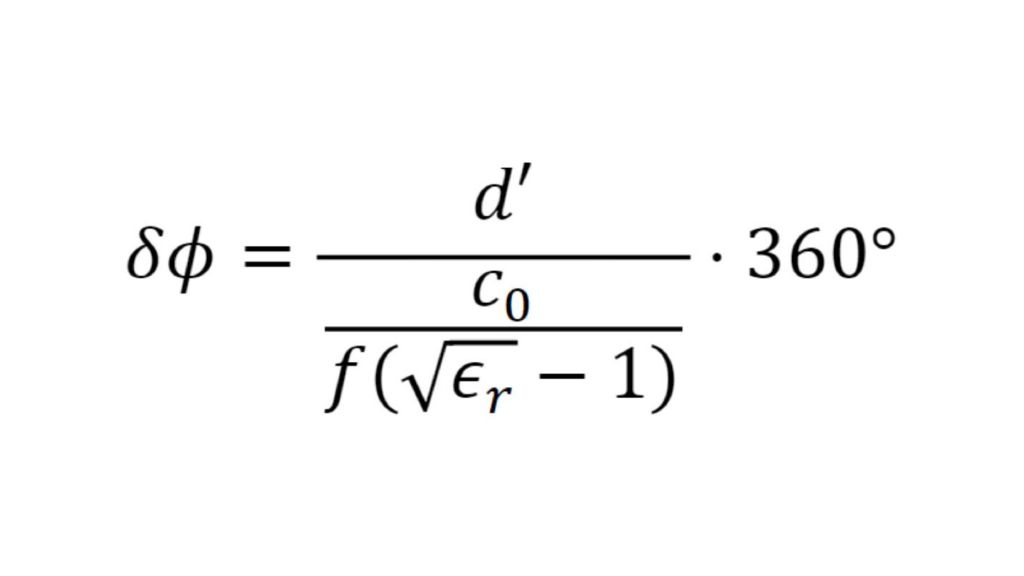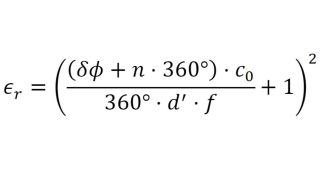Caractérisation des propriétés de matériaux polymères pour les applications automobiles

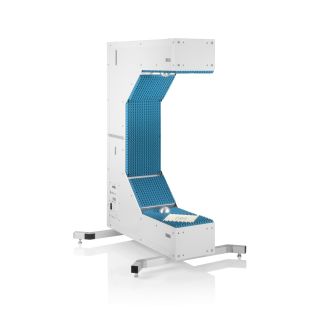
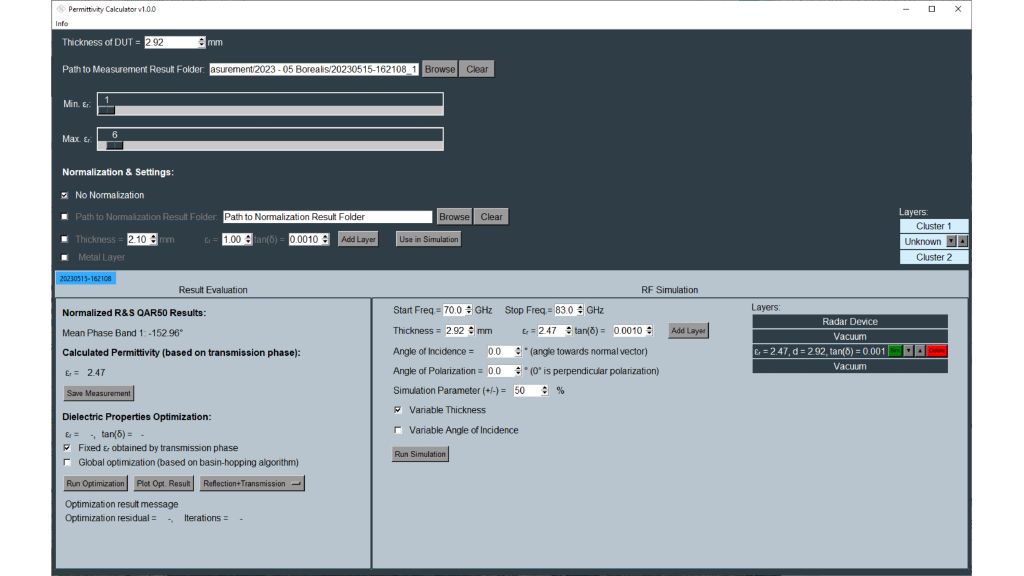
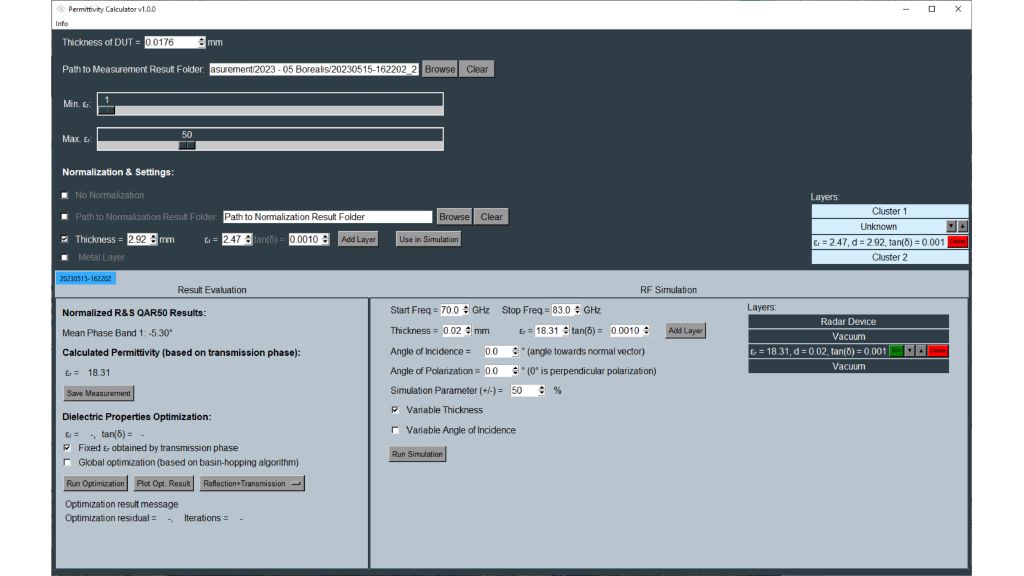
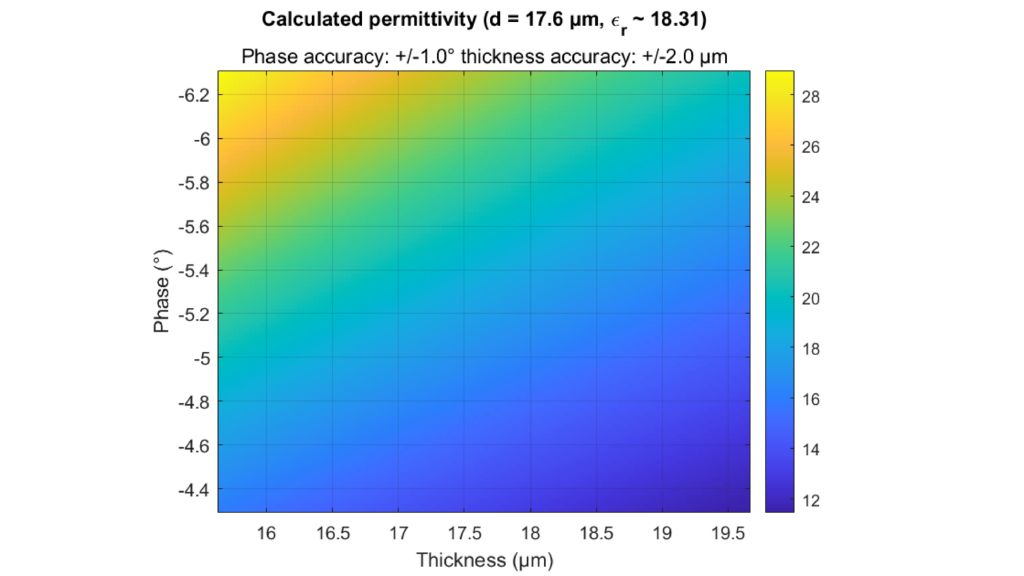
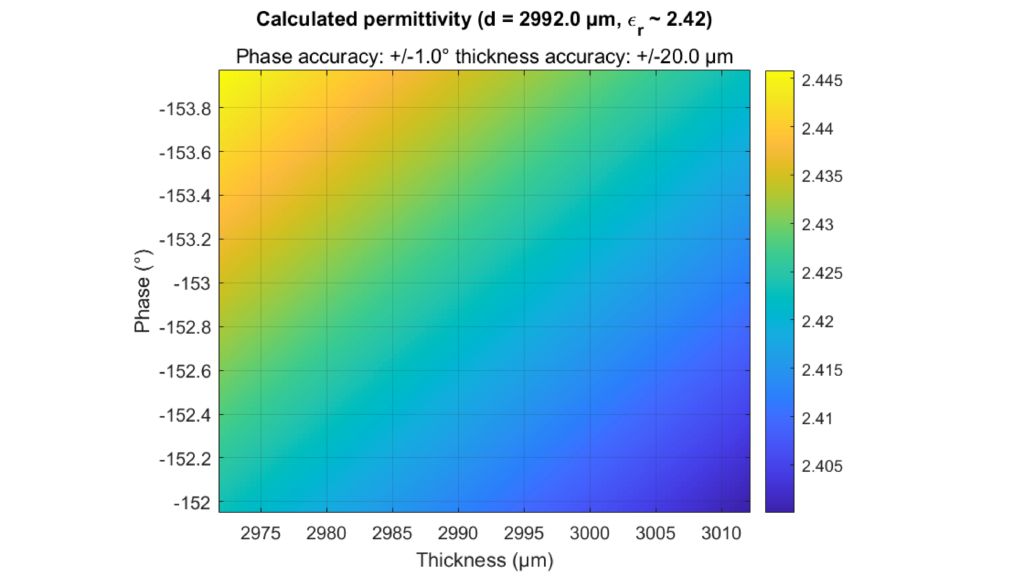
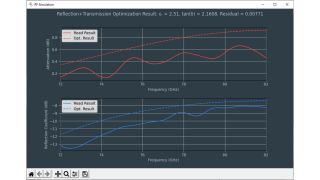
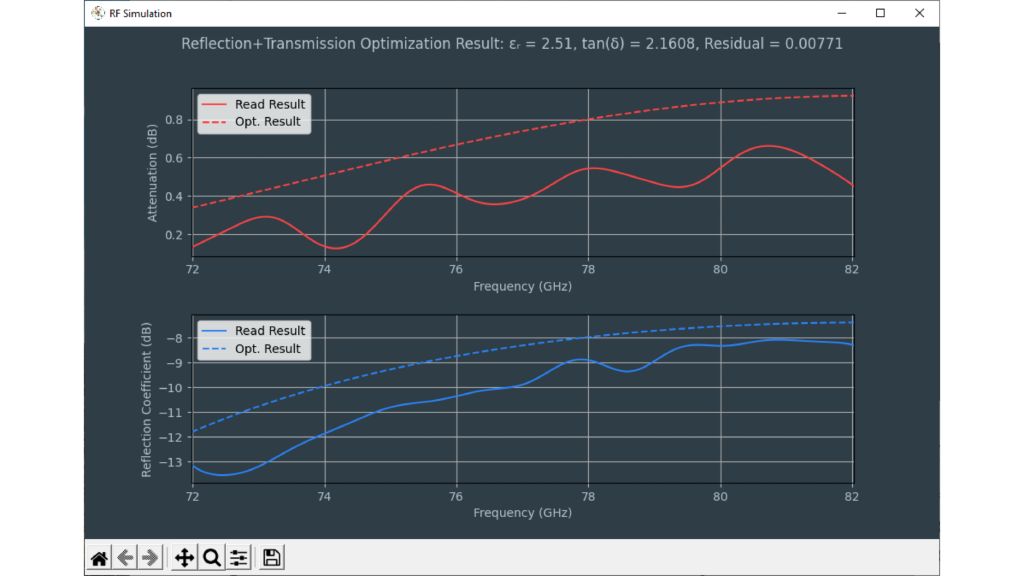
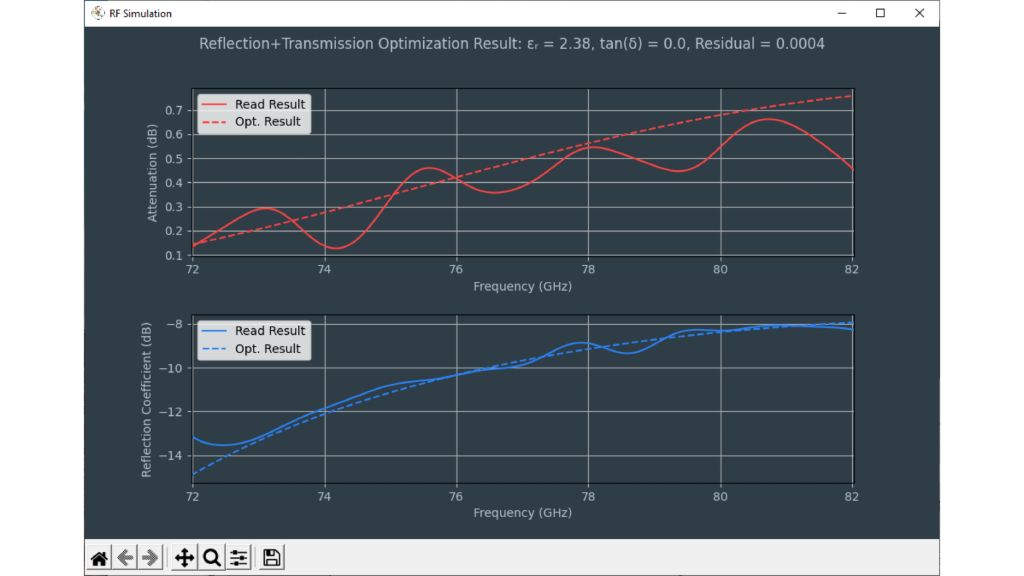
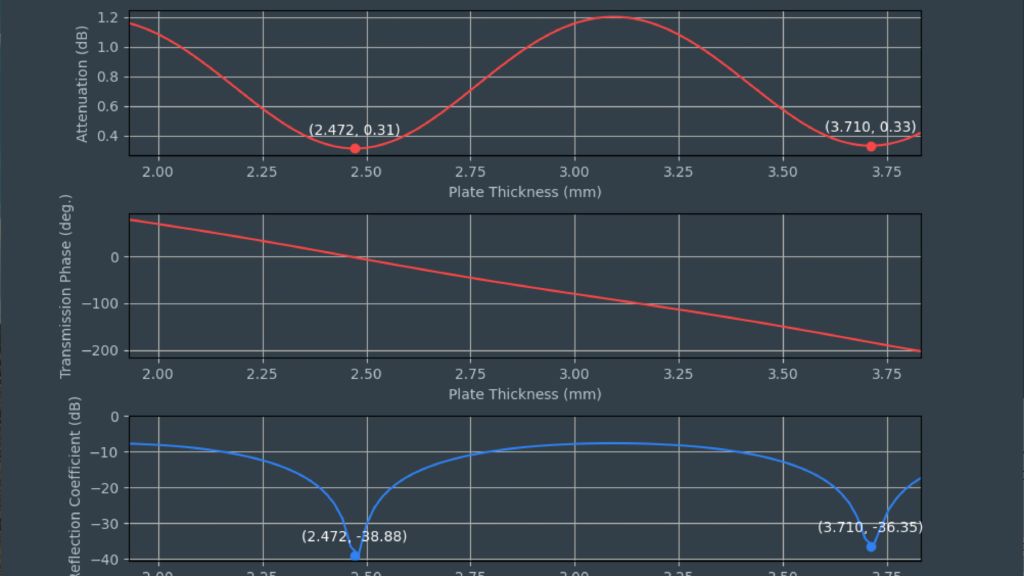
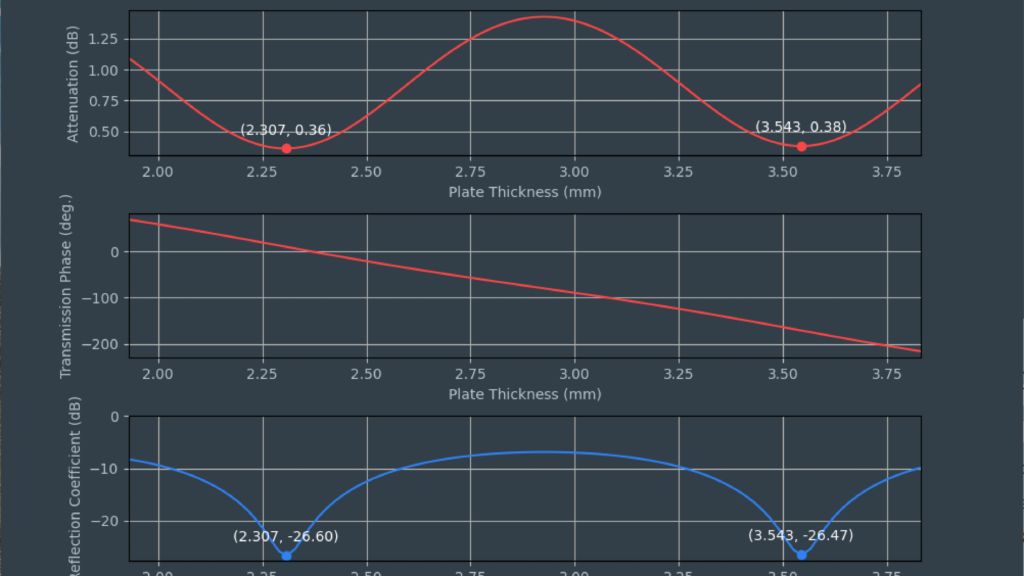
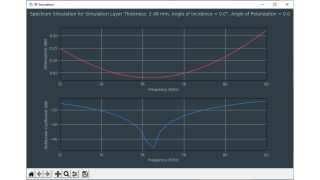
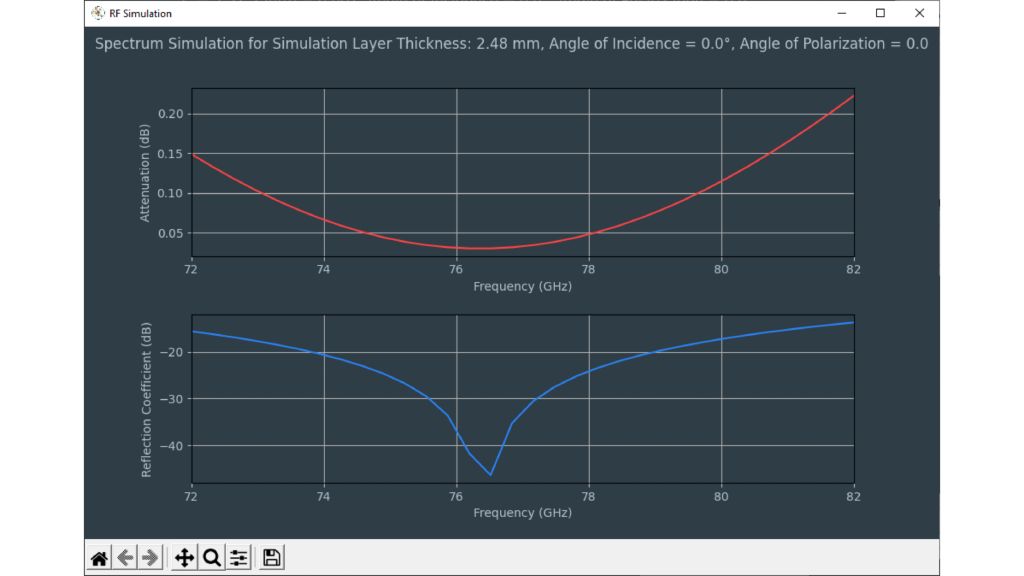
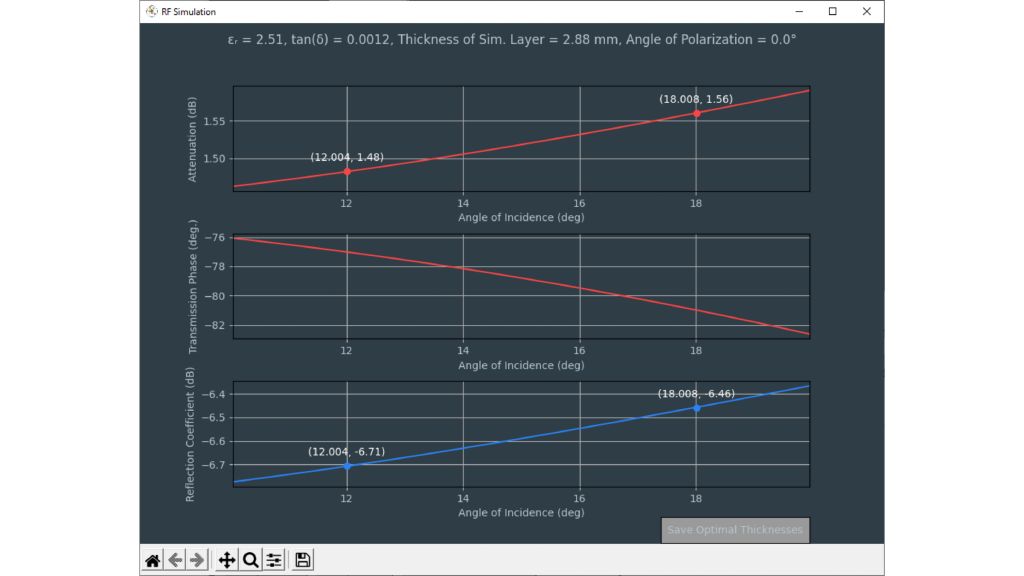
Les capteurs radar automobiles intégrés dans les pare-chocs doivent émettre dans le bon domaine fréquentiel. Afin de cacher les capteurs, des zones radar transparentes sont généralement peintes comme le reste du véhicule. Vous devez connaître les propriétés matérielles du pare-choc lors de la sélection de la peinture et des revêtements. Par le passé, des configurations quasi-optique ou à base de guides d'ondes avec des analyseurs de réseaux vectoriels (VNA) étaient utilisées. Cette carte d'application décrit une méthode de caractérisation de matériaux simplifiée dans le domaine fréquentiel des radars automobiles (76 GHz à 81 GHz) en utilisant le testeur de radômes automobiles R&S®QAR50.

Testeur de radômes automobiles R&S®QAR50
Testeur de radômes automobiles R&S®QAR50
/
Testeur de radômes automobiles R&S®QAR50

Votre tâche

Les pare-chocs automobiles possèdent généralement plusieurs couches : un matériau de base structurel, un primaire, une peinture et un revêtement transparent. Le matériau de base structurel est généralement un polypropylène (PP) ou un polycarbonate (PC) et donne au pare-choc sa forme. Le matériau de base est souvent la couche la plus épaisse mais n'influence pas nécessairement le plus les signaux radar. La couche de base peut être adaptée avec divers enduits qui lui donnent de meilleures résistance UV, rigidité, atténuation radar, etc. Le primaire est la seconde couche et permet à la peinture d'adhérer au matériau de base.

Les couches de primaire sont généralement épaisses de quelques micromètres. Une mesure d'épaisseur de cette couche et des autres peut impliquer une incertitude.

La troisième couche est la peinture appliquée sur le primaire. L'épaisseur de la couche de peinture dépend de l'opacité de la peinture mais est généralement très fine.

Pour protéger la peinture des influences environnementales, un revêtement transparent est appliqué comme quatrième et dernière couche.

L'estimation des propriétés électromagnétiques d'un pare-choc nécessite des informations relatives à l'épaisseur de chaque couche. Un microscope électronique à balayage peut déterminer leurs épaisseurs (voir Fig. 1).

Fig. 1 : Micrographie montrant les différentes couches d'un échantillon de pare-choc automobile : matériau de base (PP), primaire, peinture, vernis (de haut en bas).
Fig. 1 : Micrographie montrant les différentes couches d'un échantillon de pare-choc automobile : matériau de base (PP), primaire, peinture, vernis (de haut en bas).

Fig. 1 : Micrographie montrant les différentes couches d'un échantillon de pare-choc automobile : matériau de base (PP), primaire, peinture, vernis (de haut en bas).

/
Fig. 1 : Micrographie montrant les différentes couches d'un échantillon de pare-choc automobile : matériau de base (PP), primaire, peinture, vernis (de haut en bas).
Open Lightbox

Toutes les couches doivent être caractérisées indépendamment. La description suivante utilise quatre échantillons différents pour caractériser les quatre couches :

  • Tout d’abord, seul le matériau de base est analysé
  • Ensuite,le primaire est appliqué sur le matériau de base caractérisé, puis analysé
  • La troisième et la quatrième étape suivent la même logique d'application de la couche suivante sur la précédente

L'échantillon doit être détruit afin de créer le microgramme. Toutes les mesures ci-dessus doivent être effectuées préalablement. Le chapitre suivant examine les analyses RF nécessaires des échantillons.

Solution Rohde & Schwarz

Estimation de permittivité avec le R&S®QAR50

La permittivité d'un échantillon détermine la vitesse à laquelle les ondes électromagnétiques se déplacent à travers un matériau et à quel point la propagation de l'onde est ralentie. La réduction de la vitesse de l'onde électromagnétique réduit la longueur d'onde au sein du matériau. Avec une fréquence f et une vitesse de la lumière c0 dans le vide, la longueur d'onde λ0 est définie par :

Formule 1
Formule 1
/

Fréquence radar automobile typique : fradar = 76,5 GHz, longueur d'onde : λ0 = 3,92 mm.

La longueur d'onde au sein d'un matériau donné avec la permittivité relative εr est calculée par :

Formule 2
Formule 2
/

Prenons l'exemple d'une feuille polypropylène (PP) avec εr ~ 2,5, la longueur d'onde dans la feuille PP est calculée avec λPP = 2,34 mm. Puisque la permittivité réduit la longueur d'onde, elle peut être calculée en utilisant la phase mesurée si l'épaisseur d'un matériau sous test (MUT) est connue. La procédure générale est démontrée ci-dessous.

Calcul de la permittivité avec des différences de phase relative

Le R&S®QAR50 est normalisé pour la propagation de l'air et chaque matériau positionné entre les deux pôles altère la phase au niveau des antennes de réception. Afin de caractériser l'échantillon, nous voulons la différence de phase provenant du MUT sur le trajet de mesure.

Pour référence, la phase Φ en degrés sur une distance d dans un espace ouvert est calculée par :

Formule 3
Formule 3
/

La phase Φ’ à travers un matériau d'épaisseur d’ est calculée par :

Formule 4
Formule 4
/

Le changement de phase δΦ observé par le R&S®QAR50 est la différence entre Φ et Φ’ égaux :

Formule 5
Formule 5
/

Une feuille PVC de 2,92 mm avec une permittivité estimée εr d'environ 2,5 aura une différence de phase attendue δΦ d'environ 158°.

Comme nous mesurons la différence de phase δΦ avec le R&S®QAR50 et que nous voulons calculer la permittivité εr, la formule ci-dessus doit être convertie en :

Formule 6
Formule 6
/

La permittivité résultante n'est pas unique car la différence de phase pourrait sans le savoir être des multiples de 360°. Toutes les solutions possibles peuvent être calculées avec n Σ N0.

Lorsqu'un échantillon dispose de plusieurs couches, toutes les couches à déterminer sauf une doivent être caractérisées préalablement. Seulement ensuite, les couches connues peuvent être normalisées.

Le R&S®QAR50 dispose d'un logiciel pour simplifier les calculs. Le calculateur de permittivité utilise des résultats de mesures de phase précis provenant du R&S®QAR50 et peuvent être observés dans l'exemple ci-dessous.

Fig. 2 : La couche de base est chargée dans le calculateur de permittivité. La permittivité calculée due au changement de phase d'environ 153° à 76,5 GHz est εr = 2,47.
Fig. 2 : La couche de base est chargée dans le calculateur de permittivité. La permittivité calculée due au changement de phase d'environ 153° à 76,5 GHz est εr = 2,47.

Fig. 2 : La couche de base est chargée dans le calculateur de permittivité. La permittivité calculée due au changement de phase d'environ 153° à 76,5 GHz est εr = 2,47.

/
Fig. 2 : La couche de base est chargée dans le calculateur de permittivité. La permittivité calculée due au changement de phase d'environ 153° à 76,5 GHz est εr = 2,47.
Open Lightbox

Caractérisation d'un échantillon de pare-choc peint

En utilisant le même ensemble d'échantillons que précédemment, les épaisseurs des différentes couches sont connues et des plaques avec les couches individuelles sont disponibles pour la caractérisation. Voir Fig. 1 pour l'épaisseur des couches individuelles.

Fig. 3 : Ajout de couches de normalisation pour caractériser le primaire, la peinture et le vernis
Fig. 3 : Ajout de couches de normalisation pour caractériser le primaire, la peinture et le vernis

Fig. 3 : Ajout de couches de normalisation pour caractériser le primaire, la peinture et le vernis

/
Fig. 3 : Ajout de couches de normalisation pour caractériser le primaire, la peinture et le vernis
Open Lightbox

La plaque de base PP possède une épaisseur de 2,92 mm pour une différence de phase mesurée d'environ –153° à 76,5 GHz. En utilisant les résultats mesurés comme paramètres d'entrée, l'outil calcule une εr = 2,47 pour cette plaque spécifique. La Fig. 2 montre le résultat du calcul dans le logiciel.

En utilisant l'outil de calcul RF décrit ci-dessous, l'épaisseur optimale dopt peut être dérivée des minimas des pertes de réflexion et de transmission. Les minimas de réflexion sont corrélés à la fréquence de résonance de l'échantillon et se produisent à plusieurs multiples de la moitié de la longueur d'onde au sein du matériau :

Afin de caractériser les couches restantes, le matériau de base doit être normalisé. Puisque sa permittivité de matériau est maintenant connue, la plaque de primaire peut également être normalisée.

Une couche de normalisation est appliquée dans le logiciel et le résultats de mesure suivant est chargé.

La normalisation peut utiliser une mesure précédente ou avoir une couche avec une épaisseur et une permittivité définies ajoutées manuellement. Dans notre exemple, la couche de normalisation a une épaisseur de 2,92 mm et une εr = 2,47 est ajoutée manuellement et visualisée sur le bon côté de l'outil. En se basant sur l'épaisseur mesurée du primaire (voir Fig. 1) et sur le décalage de phase mesuré de 5,3° à partir du R&S®QAR50, la permittivité estimée pour le primaire est εr = 18,3. Le résultat peut être visualisé dans la Fig. 3.

Fig. 4 : Micrographie des trois échantillons traités
Fig. 4 : Micrographie des trois échantillons traités

Fig. 4 : Micrographie des trois échantillons traités montre des différences significatives dans l'épaisseur de certaines couches. L'échantillon #1 (PP brute) n'est pas affiché du fait de l'échelle différente.

/
Fig. 4 : Micrographie des trois échantillons traités montre des différences significatives dans l'épaisseur de certaines couches. L'échantillon #1 (PP brute) n'est pas affiché du fait de l'échelle différente.
Open Lightbox

Dès que la seconde couche est caractérisée, les couches restantes peuvent être estimées en utilisant les étapes décrites précédemment. Les couches caractérisées sont ajoutées pour la normalisation et l'outil calcule la permittivité inconnue.

Puisque les épaisseurs de couches sur les échantillons peuvent différer, soyez prudent lors de l'ajout des couches de normalisation. La Fig. 4 montre la micrographie pour les échantillons avec un microscope optique. Des différences significatives dans l'épaisseur de la couche de peinture peuvent être remarquées pour l'échantillon #3 (pour caractériser a peinture) et l'échantillon #4 (pour caractériser le vernis).

Évaluation des résultats et simulation RF

Une fois qu'un échantillon est chargé et caractérisé, l'évaluation des résultats et les zones de simulation RF en bas de l'outil apparaîtront et seront remplies automatiquement avec les valeurs spécifiques à la plaque.

“Les résultats normalisés du R&S®QAR50” montrent la phase de transmission moyenne sur la zone d'évaluation de l'échantillon sélectionné comme mesuré par le R&S®QAR50. La phase de transmission et l'épaisseur du DUT sont saisies tout en haut, la permittivité relative de l'échantillon est calculée comme décrit précédemment. Le R&S®QAR50 mesure précisément la phase de transmission mais la permittivité relative calculée dépend également de la précision de la mesure d'épaisseur.

Fig. 5 : Variation des résultats de calcul de la permittivité relative avec déviation de la mesure d'épaisseur et résultats de mesure de la déviation de phase illustrées pour un revêtement exemplaire.
Fig. 5 : Variation des résultats de calcul de la permittivité relative avec déviation de la mesure d'épaisseur et résultats de mesure de la déviation de phase illustrées pour un revêtement exemplaire.

Fig. 5 : Variation des résultats de calcul de la permittivité relative avec déviation de la mesure d'épaisseur et résultats de mesure de la déviation de phase illustrées pour un revêtement exemplaire.

/
Fig. 5 : Variation des résultats de calcul de la permittivité relative avec déviation de la mesure d'épaisseur et résultats de mesure de la déviation de phase illustrées pour un revêtement exemplaire.
Open Lightbox

Influence d'une mesure imprécise
Soyez prudent avec les mesures d'épaisseur car les deux valeurs ont une influence majeure sur la permittivité calculée. Les Figs. 5 et 6 illustrent l'impact de mesures de transmission de phase et / ou d'épaisseur imprécises. En se basant sur les mesures précédentes, un revêtement avec une épaisseur de d = 17,6 µm et un décalage de phase de ∆φ = –5,3° engendrent une permittivité avec un εr d'environ 18,3. Afin d'illustrer l'influence des mesures de phase et d'épaisseur imprécises, les deux paramètres sont évalués avec des précisions de mesure typiques : ±2 µm pour la mesure d'épaisseur et ±1° pour la phase de transmission. La Fig. 5 montre comment la permittivité relative calculée résultante varie énormément lorsque les résultats de mesure deviennent encore plus imprécis. Faîtes attention lors de la mesure des caractéristiques RF d'un matériau et lors de la détermination de l'épaisseur de couches.

Fig. 6 : Variation des résultats de calcul de la permittivité relative avec des résultats de mesure de déviation d'épaisseur et de mesure de déviation de phase illustrés pour un substrat échantillon.
Fig. 6 : Variation des résultats de calcul de la permittivité relative avec des résultats de mesure de déviation d'épaisseur et de mesure de déviation de phase illustrés pour un substrat échantillon.

Fig. 6 : Variation des résultats de calcul de la permittivité relative avec des résultats de mesure de déviation d'épaisseur et de mesure de déviation de phase illustrés pour un substrat échantillon.

/
Fig. 6 : Variation des résultats de calcul de la permittivité relative avec des résultats de mesure de déviation d'épaisseur et de mesure de déviation de phase illustrés pour un substrat échantillon.
Open Lightbox

Dans la Fig. 6, le substrat échantillon possède une permittivité de 2,42 et une épaisseur de 2,92 mm. Un micromètre a été utilisé pour cette mesure d'épaisseur et l'incertitude de mesure modifiée à ±20µm. La précision de la phase reste identique car le même appareil avait été utilisé pour la mesure.

L'effet est moins significatif pour les matériaux avec une permittivité plus faible et une épaisseur significativement plus importante que l'incertitude de mesure (par exemple PC ou PP).

Optimisation de la propriété diélectrique
La permittivité et le facteur de perte doivent être connus pour simuler des matériaux et des superpositions de matériaux et créer un duplicata virtuel d'un radôme. La permittivité relative εr est corrélée avec le facteur de compression de la longueur d'onde au sein du matériau, tandis que la tan δ (facteur de pertes) caractérise l'atténuation spécifique d'un signal émis depuis la couche.

Le calculateur de permittivité Rohde & Schwarz peut être utilisé pour les deux paramètres et est idéal pour les simulations de couche de radôme.

Les outils pour l'estimation des propriétés diélectriques sont dans le coin inférieur gauche du logiciel de calcul de la permittivité. Le calculateur utilise un optimiseur pour trouver le meilleur ajustement entre les réponses en fréquence mesurée et calculée en se basant sur la permittivité et les facteurs de perte. Les utilisateurs peuvent choisir entre différentes méthodes de calcul en vérifiant :

  • Le mode “Fixed εr obtained by transmission phase” optimise uniquement la tan δ tandis que la permittivité relative reste fixe
  • Non vérifié, l'optimiseur a plus de liberté pour améliorer la permittivité relative; la permittivité relative calculée à partir de la phase de transmission agit comme la valeur initiale

Les deux méthodes ont des résultats similaires pour la plupart des matériaux. La phase de transmission peut être mesurée très précisément et est toujours un très bon point de départ de l'optimisation.

“Optimiser en utilisant l'échelle logarithmique (dB)” règle l'optimiseur pour qu'il travaille avec une courbe logarithmique afin d'augmenter la précision de l'estimation pour des matériaux avec une résonance dans la bande de fréquence du R&S®QAR50.

Une optimisation globale utilise plusieurs points de démarrage distribués aléatoirement à proximité de la valeur de permittivité calculée afin d'éviter une optimisation à un minimum local.

Les courbes de réflexion des cluster 1 (S11) ou cluster 2 (S22) sont disponibles pour des applications spécifiques au client.

Fig. 7 : Optimisation des résultats avec une valeur de permittivité fixe
Fig. 7 : Optimisation des résultats avec une valeur de permittivité fixe

Fig. 7 : Optimisation des résultats avec une valeur de permittivité fixe

/
Fig. 7 : Optimisation des résultats avec une valeur de permittivité fixe
Open Lightbox

Les réponses en fréquence mesurée et calculée peuvent être tracées après l'exécution de l'optimisation. La fonction “Plot Opt. Results” trace la réponse en fréquence pour le matériau mesuré (ligne continue) ainsi que le matériau virtuel (ligne pointillée) en utilisant des propriétés de matériau calculées précédemment. Les opérateurs doivent vérifier la validité des résultats pour les deux méthodes. Les Figs. 7 et 8 montrent les graphiques générés. La Fig. 7 a été créée en utilisant la permittivité fixe de la phase de transmission. La Fig. 8 a été créée en optimisant à la fois la permittivité et les tangentes de pertes pour une réponse en fréquence la plus adaptée.

Fig. 8 : Optimisation des résultats avec une permittivité optimisée et le facteur de perte
Fig. 8 : Optimisation des résultats avec une permittivité optimisée et le facteur de perte

Fig. 8 : Optimisation des résultats avec une permittivité optimisée et le facteur de perte

/
Fig. 8 : Optimisation des résultats avec une permittivité optimisée et le facteur de perte
Open Lightbox

Le matériau précédemment mesuré avec le R&S®QAR50 est utilisé comme un exemple afin d'estimer le facteur de perte.

En tant que guide général, l'erreur d'optimisation résiduelle est indiquée dans le diagramme. Plus l'erreur est faible, plus l'ajustement est bon. L'optimisation à la fois de la permittivité et du facteur de perte est légèrement plus adaptée à notre exemple. Les résultats d'évaluation peuvent être utilisés pour des simulations dans l'outil d'optimisation de couche.

Fig. 9 : Résultat de simulation RF d'une feuille de matériau avec εr = 2,51 et tan δ = 0,0012
Fig. 9 : Résultat de simulation RF d'une feuille de matériau avec εr = 2,51 et tan δ = 0,0012

Fig. 9 : Résultat de simulation RF d'une feuille de matériau avec εr = 2,51 et tan δ = 0,0012

/
Fig. 9 : Résultat de simulation RF d'une feuille de matériau avec εr = 2,51 et tan δ = 0,0012
Open Lightbox
Outil d'optimisation de couche

L'outil d'optimisation de couche du côté droit du calculateur de permittivité est activé avec le chargement d'une mesure valide du R&S®QAR50. L'outil permet de simuler plusieurs couches de peinture et d'évaluer l'effet de n'importe quelle différence dans l'épaisseur de couche.

Les fréquences de départ et de fin représentent des bandes radar utilisées pour une application. Un jumeau numérique d'une partie est créé avec les paramètres matériau enregistrés précédemment pour une seule feuille de couche. Le bouton “calculate optimal thickness” peut être utilisé pour une simulation RF des couches. Les résultats de calcul pour le matériau échantillon et l'épaisseur peuvent être visualisés en Fig. 9

Dans la Fig. 9 l'épaisseur optimale pour une seule feuille de couche est 2,47 mm. L'épaisseur s'applique aux couvercles radar non peints. Pour simplifier, supposons qu'une seule couche ait été appliquée au matériau de base au lieu de trois couches (primaire, peinture et revêtement). La couche ajoutée est d'une épaisseur d = 20 µm et a une εr = 15 avec une tan δ = 0,02. La couche représente une peinture typique utilisée dans l'industrie automobile.

Fig. 10 : Simulation de la feuille avec une couche de peinture supplémentaire
Fig. 10 : Simulation de la feuille avec une couche de peinture supplémentaire

Fig. 10 : Simulation de la feuille avec une couche de peinture supplémentaire (d = 20 μm, εr = 15 et d tan δ = 0,02

/
Fig. 10 : Simulation de la feuille avec une couche de peinture supplémentaire (d = 20 μm, εr = 15 et d tan δ = 0,02
Open Lightbox

Le défi est toujours le même : Nous voulons une épaisseur optimale sur le matériau de base pour une couche de peinture. Après l'ajout de la couche de l'outil de simulation RF, nous pouvons effectuer les mêmes calculs qu'à la Fig. 9. Supposons que l'épaisseur de la couche de peinture soit fixe et que l'épaisseur optimale pour la couche de base soit nécessaire. La Fig. 10 montre le résultat d'une simulation RF.

Fig. 11 : Réponse en fréquence d'une couche simulée avec permittivité relative 2,5 et épaisseur 2,48 mm.
Fig. 11 : Réponse en fréquence d'une couche simulée avec permittivité relative 2,5 et épaisseur 2,48 mm.

Fig. 11 : Réponse en fréquence d'une couche simulée avec permittivité relative 2,5 et épaisseur 2,48 mm.

/
Fig. 11 : Réponse en fréquence d'une couche simulée avec permittivité relative 2,5 et épaisseur 2,48 mm.
Open Lightbox

La couche a une permittivité élevée et une influence majeure sur la performance radar malgré sa finesse et l'effet peut être observé dans la simulation. Au lieu de 2,47 mm pour la feuille non peinte, 2,31 mm serait l'épaisseur idéale.

La même procédure s'applique à toutes les couches restantes et l'épaisseur du pare-choc (ou des autres couches) peut être optimisée

Une autre fonctionnalité utile peut être activée en survolant un point d'épaisseur spécifique dans le diagramme et en appuyant sur “n”. Cela créera un tracé de fréquence résolue pour cette épaisseur spécifique. La gamme de fréquence est définie par l'utilisateur dans la fenêtre principale du calculateur de permittivité.

Fig. 12 : Simulation d'angles d'installation typiques du cache radar simplifié évoqué préalablement
Fig. 12 : Simulation d'angles d'installation typiques du cache radar simplifié évoqué préalablement

Fig. 12 : Simulation d'angles d'installation typiques du cache radar simplifié évoqué préalablement

/
Fig. 12 : Simulation d'angles d'installation typiques du cache radar simplifié évoqué préalablement
Open Lightbox

Les résultats de simulation décrits ci-dessus peuvent être calculés pour des épaisseurs et des angles de simulation variants. En s'appuyant sue une feuille peinte simplifiée, l'angle d'installation du cache par rapport au radar impacte la performance. Le logiciel calculateur de permittivité peut être utilisé pour déterminer cet effet.

La variation de l'angle d'installation de 10° à 20° (représentant les angles d'installation typiques de l'automobile) révèle clairement l'effet de l'angle d'incidence.

L'angle d'incidence et la polarisation du champ électrique par rapport à l'angle d'incidence impacte l'épaisseur optimale et l'optimisation. Le calculateur de permittivité peut être utilisé pour simuler les effets de l'angle de polarisation de l'onde électromagnétique entrante. 0° correspond à une polarisation perpendiculaire entre le plan d'incidence et le champ électrique de l'onde électrique entrante

Conclusion

Lorsqu'il est combiné avec le R&S®QAR50, le calculateur de permittivité est l'outil idéal pour la caractérisation sans fil des matériaux. En se basant sur les mesures des pertes de transmission, de phase et de réflexion, la permittivité relative et le facteur de perte du matériau sous test peuvent être calculés. En utilisant le puissant outil de simulation RF, l'épaisseur de toutes les couches peut être adaptée pour un radôme bien ajusté dans la gamme de fréquence des radars automobiles.

Le logiciel calculateur de permittivité peut être téléchargé gratuitement sur le site internet du R&S®QAR50 :

www.rohde-schwarz.com/de/software/qar50/

Téléchargements